Solving the Spiral Matrix Generation Problem
What is a Spiral Matrix?
A spiral matrix is a fascinating algorithmic challenge where we create a square matrix filled with consecutive numbers, starting from 1, arranged in a clockwise spiral pattern. Imagine filling a grid by moving in a spiral, starting from the top-left corner and moving outwards in a clockwise direction.
Problem Statement
Given a positive integer n, your task is to generate an n x n matrix where:
- The matrix contains all numbers from 1 to n²
- Numbers are filled in a clockwise spiral order
- The matrix starts filling from the top-left corner
Problem Constraints:
1 <= A <= 1000
Example Input
Input1: 1
Output 1:
[ [1] ]
Input2: 2
Output 2:
[ [1, 2],
[4, 3] ]
Input3: 5
Output 3:
[ [1, 2, 3, 4, 5],
[16, 17, 18, 19, 6],
[15, 24, 25, 20, 7],
[14, 23, 22, 21, 8],
[13, 12, 11, 10, 9] ]
Visual Examples
Let’s look at some concrete examples to understand the pattern:
If n=3 then 3×3 Matrix Example

If n = 4 then 4×4 Matrix Example

Algorithm Breakdown
The key to solving this problem is understanding the directional movement:
- Initial Setup
- Create an empty n × n matrix
- Start at the top-left corner (0,0)
- Begin with the first number (1)
- Movement Directions The algorithm uses four primary directions:
- Right: Move horizontally (increasing column)
- Down: Move vertically downwards (increasing row)
- Left: Move horizontally backwards (decreasing column)
- Up: Move vertically upwards (decreasing row)
- Direction Changing Strategy
- Change direction when:
- Reaching matrix boundaries
- Encountering an already filled cell
- Change direction when:
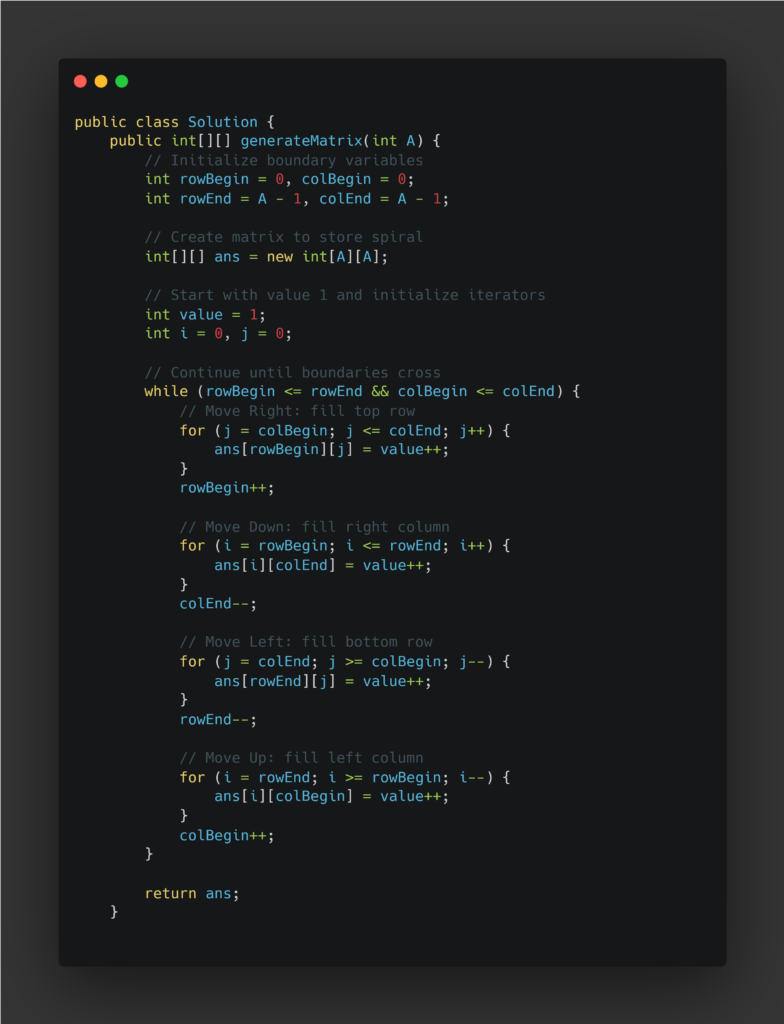
Java Implementation
Here’s a clean and efficient implementation
Time and Space Complexity
I’ll help you analyze the time and space complexity of the spiral matrix generation algorithm. However, I noticed that the Java code you mentioned is not present in your message. Could you please provide the Java code so I can review it in detail?
Without seeing the specific implementation, I can confirm that your analysis of the time and space complexity seems sound based on the description:
Time Complexity: O(n²)
- The algorithm fills each position in an n × n matrix exactly once
- The total number of operations is n²
- Each element is visited and assigned a value once
Space Complexity: O(n²)
- The output matrix requires n × n space to store all elements
- Additional variables use constant extra space
- The space used directly scales with the input size n²
If you could share the Java code, I can provide a more detailed and precise analysis of its specific implementation. Would you like to paste the code for me to review?
Conclusion
Spiral matrix generation might seem complex at first, but with a systematic approach, it becomes an elegant problem showcasing clever algorithmic thinking.

