487. Max Consecutive Ones II

Given a binary array nums, return the maximum number of consecutive 1‘s in the array if you can flip at most one 0.

Example 1:

Input: nums = [1,0,1,1,0]
Output: 4
Explanation: 
- If we flip the first zero, nums becomes [1,1,1,1,0] and we have 4 consecutive ones.
- If we flip the second zero, nums becomes [1,0,1,1,1] and we have 3 consecutive ones.
The max number of consecutive ones is 4.

Example 2:

Input: nums = [1,0,1,1,0,1]
Output: 4
Explanation: 
- If we flip the first zero, nums becomes [1,1,1,1,0,1] and we have 4 consecutive ones.
- If we flip the second zero, nums becomes [1,0,1,1,1,1] and we have 4 consecutive ones.
The max number of consecutive ones is 4.

Constraints:

• 1 <= nums.length <= 105
• nums[i] is either 0 or 1.

Problem Intuition

The goal is to find the longest stretch of consecutive 1s in a binary array, but with one twist: you are allowed to flip at most one 0 into a 1.

How the Two-Pointer Approach Works

Think of it as a Sliding Window:

• We use two pointers, left (l) and right (r), to represent the current “window” of the array we’re analyzing.
• This window will always contain at most one 0 flipped to a 1.

Track Zeros in the Window:

• We keep a counter k, which starts at 1 (because we can flip one 0).
• Each time we encounter a 0 in our window, we “spend” this flip by decrementing k.

When the Window Becomes Invalid:

• If k becomes negative, it means we’ve encountered more than one 0 in the window. At this point, the window is invalid.
• To fix this, we shrink the window by moving the left pointer (l) to the right, until the window contains at most one 0 (i.e., k is no longer negative).

Keep Expanding the Window:

• As the right pointer (r) moves forward, and the window continues to expand. If it becomes invalid, we adjust the left pointer (l) as described above.

Track the Largest Window:

• At every step, the size of the window (r - l) represents the number of consecutive 1s (with at most one 0 flipped). By the end of the iteration, this will naturally give us the longest sequence.

Key Idea

We don’t explicitly store a “maximum length” variable. Instead:

• The size of the window grows as we expand r.
• It only shrinks temporarily when k becomes negative, and then it resumes expanding once the window is valid again.
• This ensures the longest window is automatically tracked.

Explanation with Example

Imagine the array: [1, 0, 1, 1, 0, 1, 1, 1]

• Start with l = 0, r = 0, k = 1.
• As r moves:
  • At r = 1, you encounter a 0. Decrement k to 0.
  • At r = 4, you encounter another 0. Decrement k to -1. Now the window is invalid.
  • Move l to the right until the window becomes valid again (k = 0).

By the end of the loop, the largest window size (r - l) will give you the result.

Final Code Here:

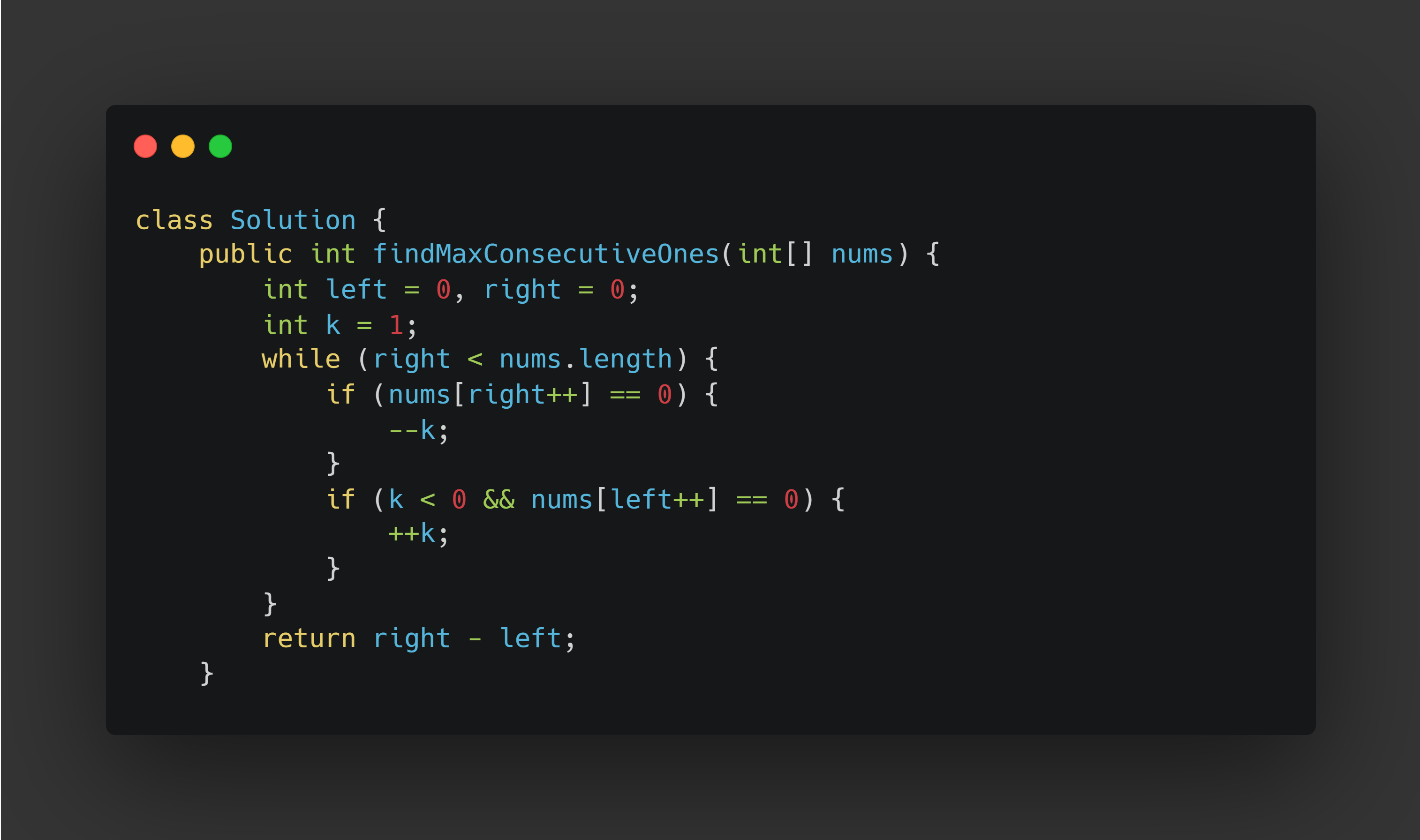
Time and Space Complexity

The time complexity of the given code is O(n), where n is the length of the input list nums. This efficiency is achieved because the code uses a two-pointer technique that iterates through the list only once. The pointers l (left) and r (right) move through the array without making any nested loops, thus each element is considered only once during the iteration.

The space complexity of the code is O(1), which means it uses constant additional space regardless of input size. No extra data structures that grow with the input size are used; the variables left, right, and k take up a constant amount of space.